DFS on Binary Tree Array

Implementing Depth-First Search for the Binary Tree without stack and recursion.

Binary Tree Array

This is binary tree.

img

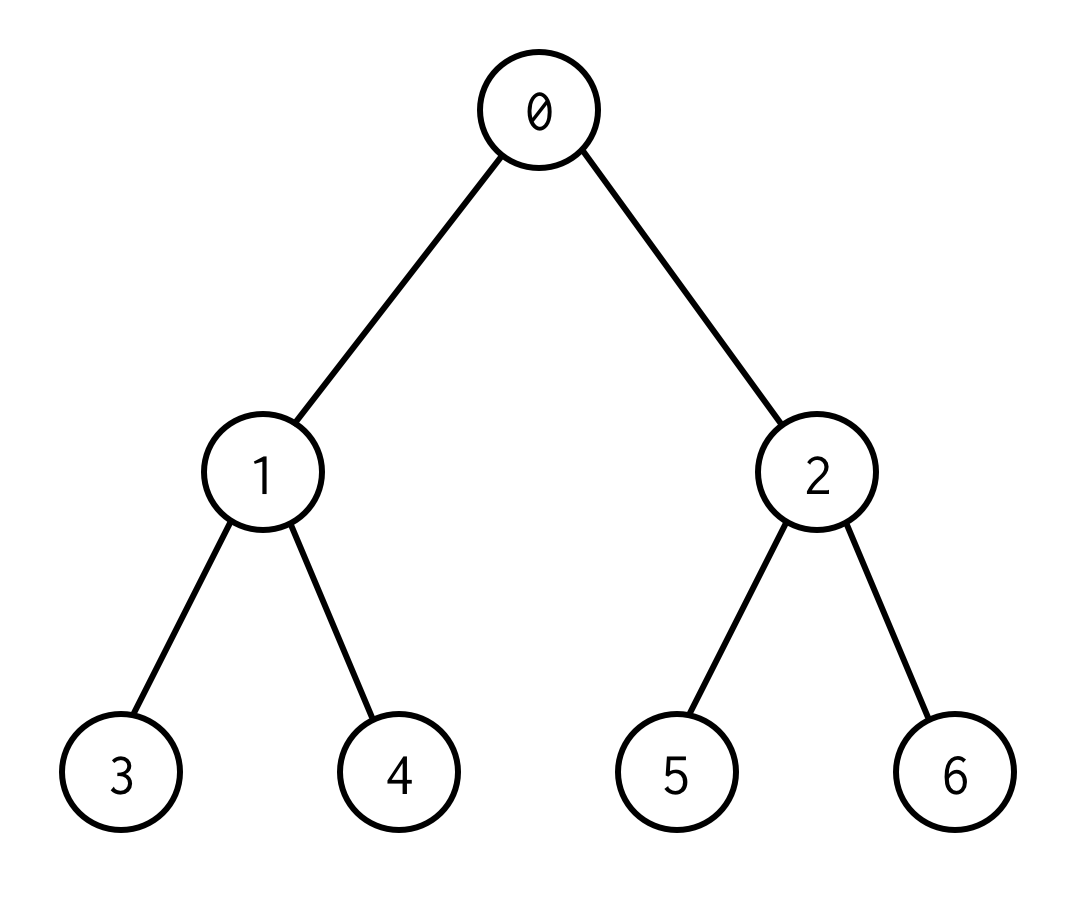
0 is a root node.
0 has two children: left 1 and right: 2.
Each of its children have their children and so on.
The nodes without children are leaf nodes (3,4,5,6).

The number of edges between root and leaf nodes define tree height. The tree above has the height 2.

Standard approach to implement binary tree is to define class called BinaryNode

public class BinaryNode<T> {
    public T data;
    public BinaryNode<T> left;
    public BinaryNode<T> right;
}

However, there is a trick to implement binary tree using only static arrays. If you enumerate all nodes in binary tree by levels starting from zero you can pack it into array.

img

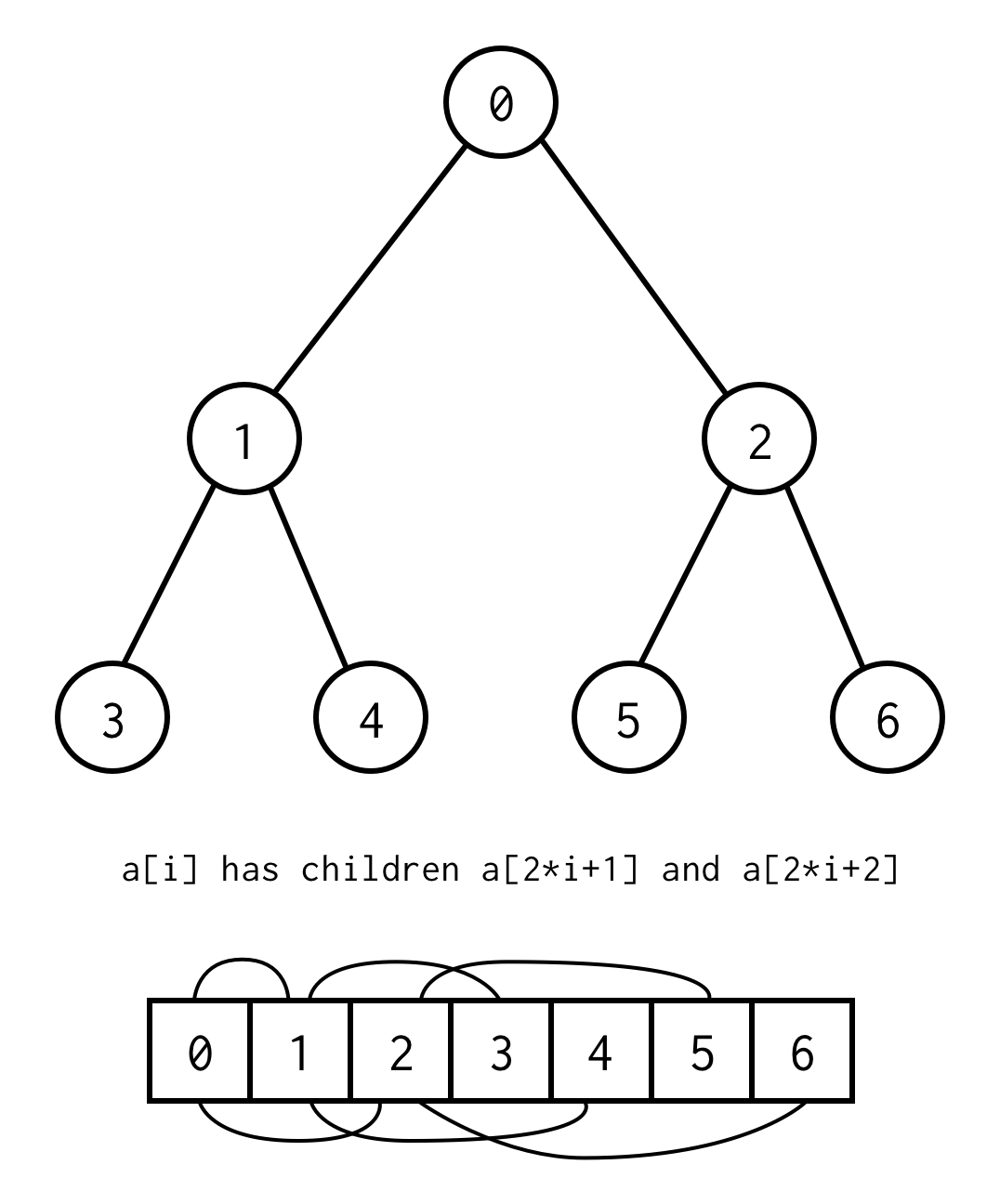
The relationship between parent index and child index, allow us to move from the parent to child, as well as from the child to the parent

left_child(i)  = 2 * i + 1
right_child(i) = 2 * i + 2
parent(i)      = (i - 1) / 2

Important note that the tree should be complete, what means for the specific height it should contain exactly \(2^{height + 1} - 1\) elements.

You can avoid such requirement by placing null instead of missing elements. The enumeration still applies for empty nodes as well. This should cover any possible binary tree.

img

Such array representation for binary tree we will call Binary Tree Array. We always assume it will contain \(2^{n} - 1\) elements.

BFS vs DFS

There are two search algorithms exist for binary tree: breadth-first search (BFS) and depth-first search (DFS).

The best way to understand them is visually

img

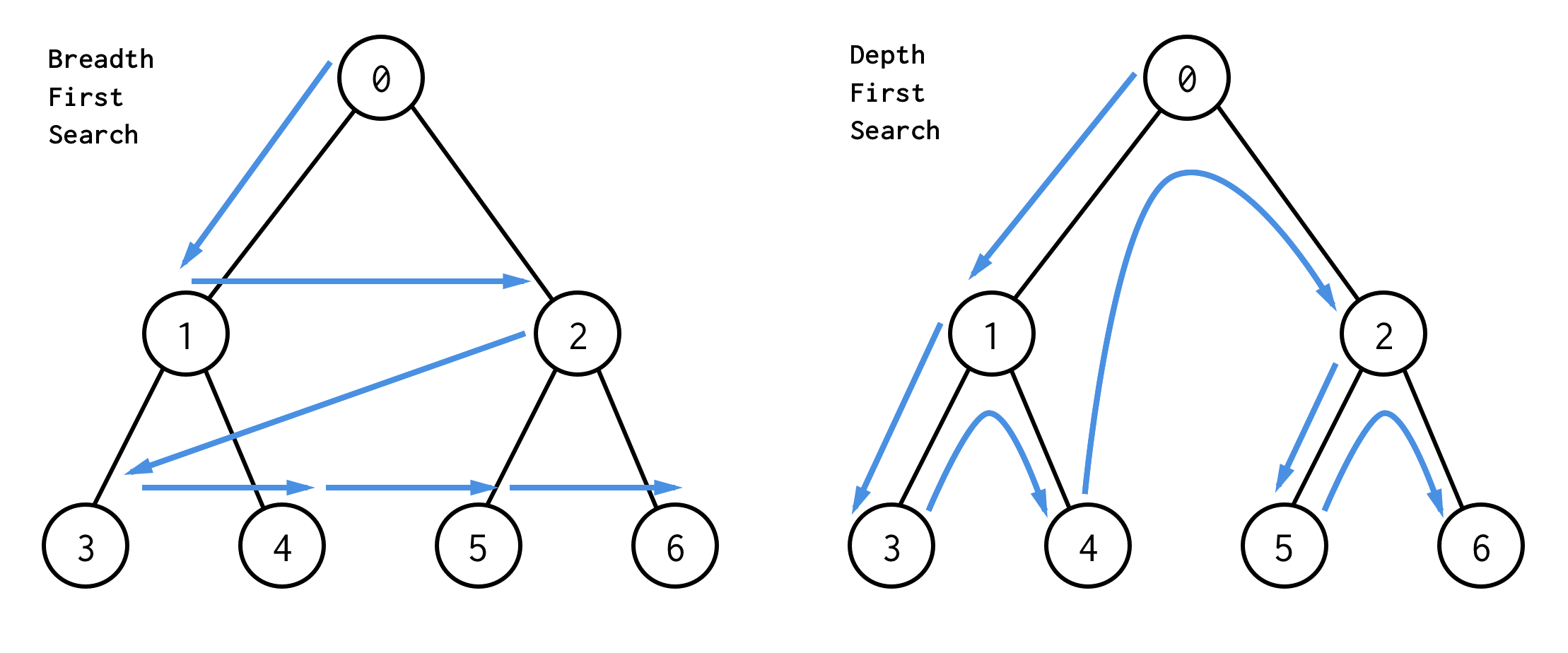
BFS search nodes level by level, starting from the root node. Then checking its children. Then children for children and so on. Until all nodes are processed or node which satisfies search condition is found.

DFS behave differently. It checks all nodes from leftmost path from the root to the leaf, then jumps up and check right node and so on.

For classic binary trees BFS implemented using Queue data structure (LinkedList implements Queue)

public BinaryNode<T> bfs(Predicate<T> predicate) {
    Queue<BinaryNode<T>> queue = new LinkedList<>();
    queue.offer(this);
    while (!queue.isEmpty()) {
        BinaryNode<T> node = queue.poll();
        if (predicate.test(node.data)) return node;
        if (node.left != null) queue.offer(node.left);
        if (node.right != null) queue.offer(node.right);
    }
    return null;
}

If you replace queue with the stack you will get DFS implementation.

public BinaryNode<T> dfs(Predicate<T> predicate) {
    Stack<BinaryNode<T>> stack = new Stack<>();
    stack.push(this);
    while (!stack.isEmpty()) {
        BinaryNode<T> node = stack.pop();
        if (predicate.test(node.data)) return node;
        if (node.right != null) stack.push(node.right);
        if (node.left != null) stack.push(node.left);
    }
    return null;
}

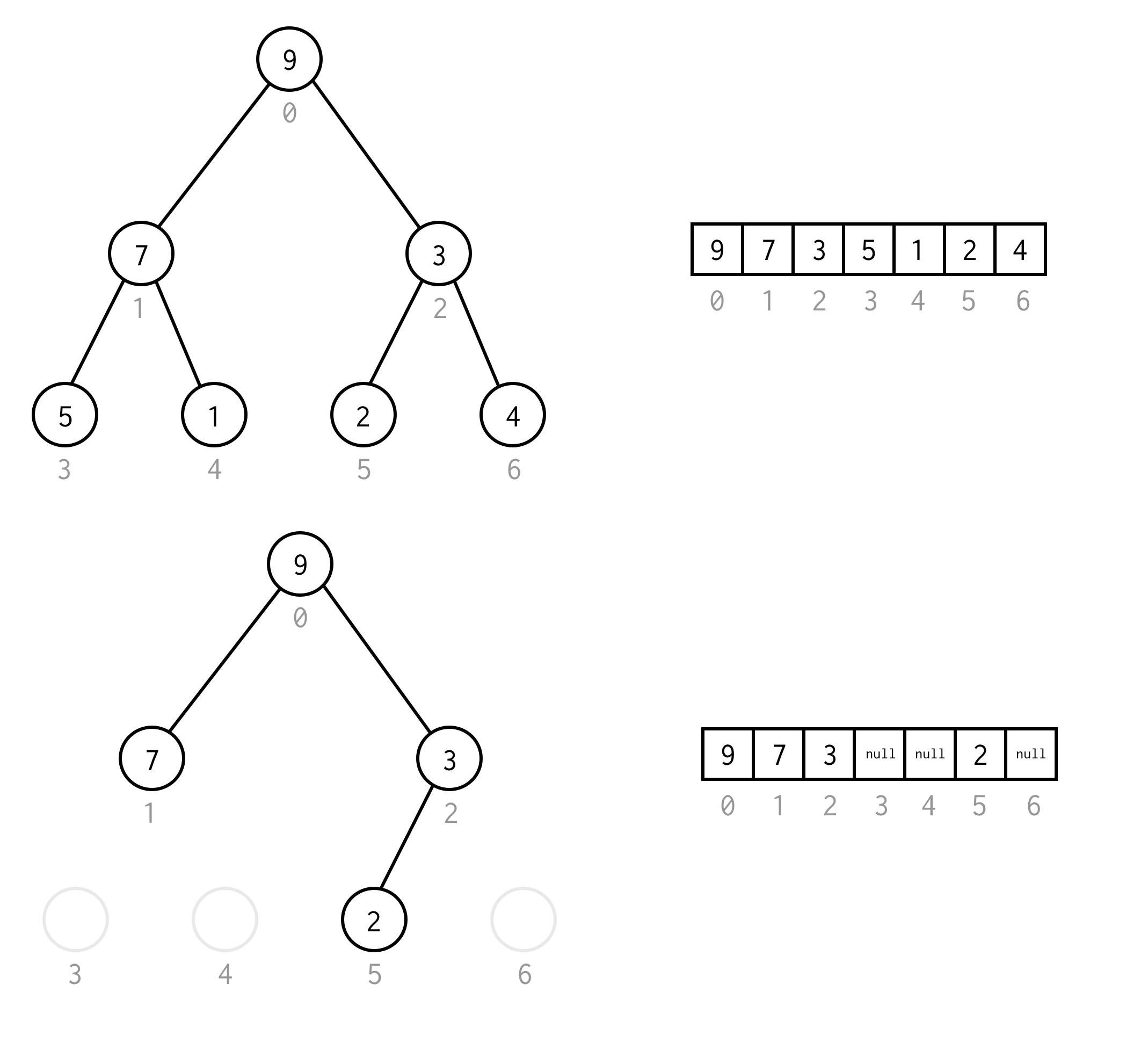
For example, assume you need to find node with value 1 in the following tree.

img

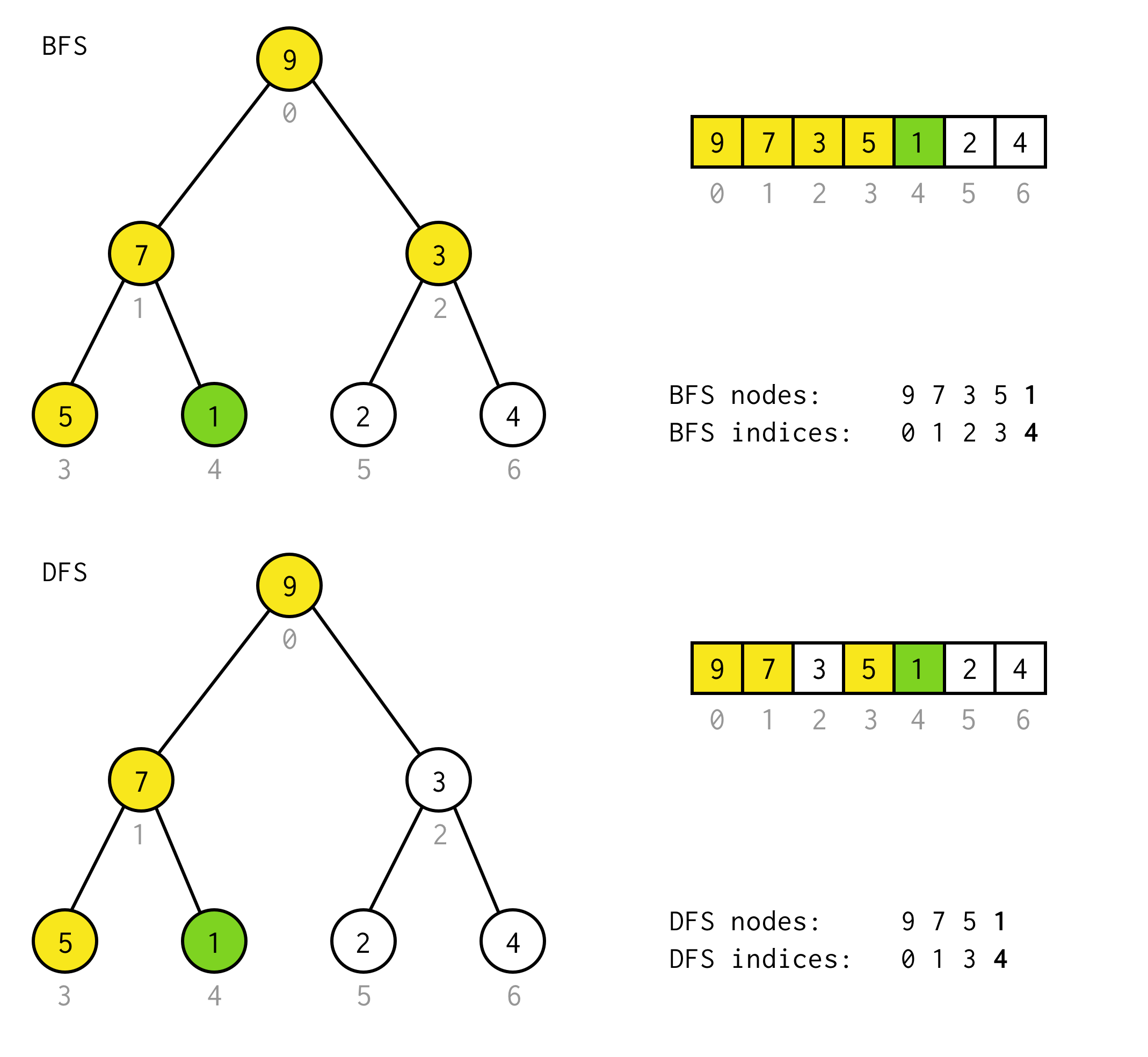
Yellow cell are cells which are tested in search algorithm before needed node found. Take into account that for some cases DFS require less nodes for processing. For some cases it requires more.

BFS and DFS for Binary Tree Array

Breadth-first search for binary tree array is trivial. Since elements in binary tree array are placed level by level and bfs is also checking element level by level, bfs for binary tree array is just linear search

public int bfs(Predicate<T> predicate) {
    for (int i = 0; i < array.length; i++) {
        if (array[i] != null && predicate.test(array[i])) return i;
    }
    return -1; // not found
}

Depth-first search is a bit harder.

Using stack data structure it could be implemented the same way as for classic binary tree, just put indices into the stack.

From this point recursion is not different at all, you just use implicit method call stack instead of data structure stack.

What if we could implement DFS without stack and recursion. In the end is just a selecting correct index on each step?

Well, let’s try.

DFS for Binary Tree Array (without stack and recursion)

As in BFS we start from the root index 0.
Then we need to inspect its left child, which index could be calculated by formula 2*i+1.
Let’s call process of going to next left child doubling.

img

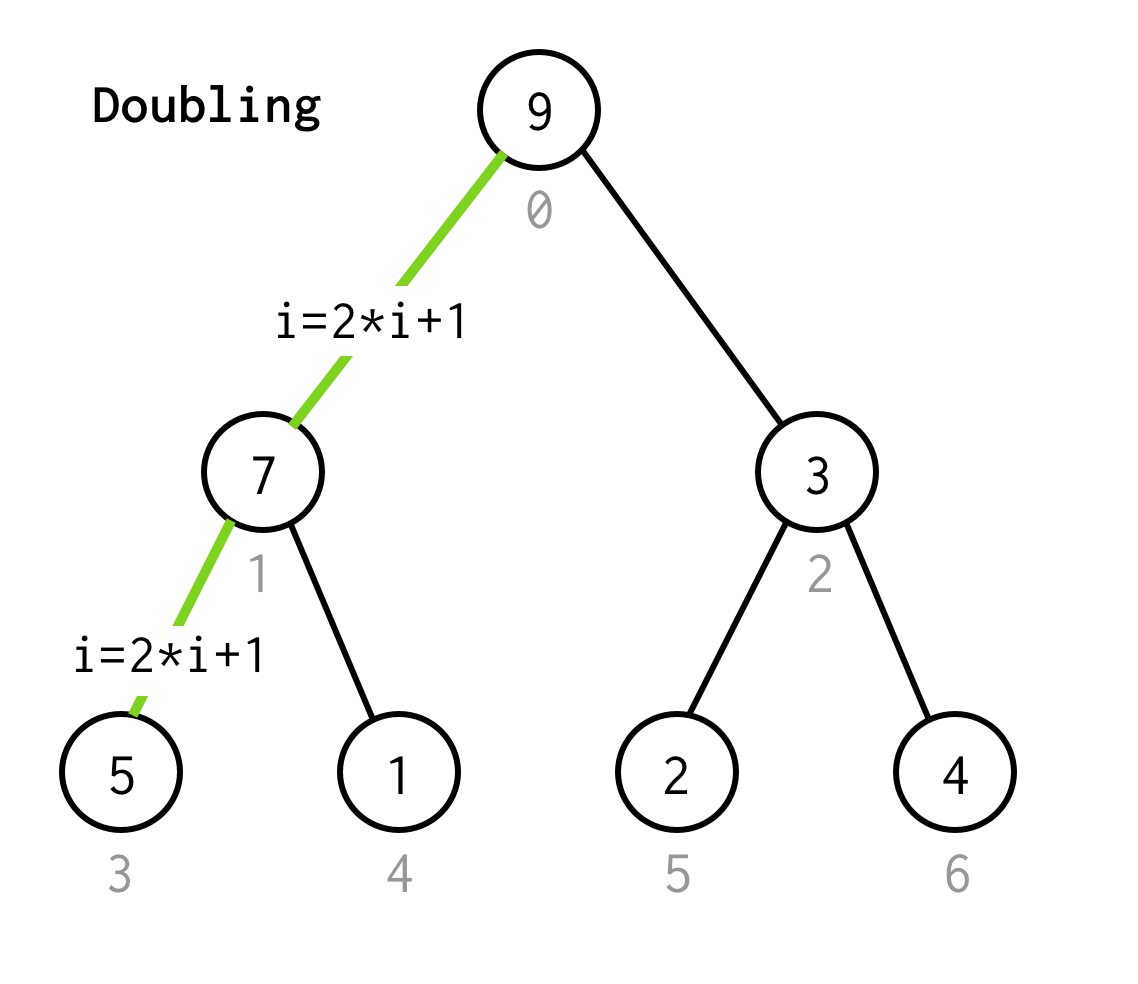
We continue doubling the index until we don’t stop at the leaf node.

So how can we understand it’s a leaf node?

If next left child produce index out of array bounds exception we need to stop doubling and jump to the right child.

That’s a valid solution, but we can avoid unnesessary doubling. The observation here is the number of elements in the tree of some height is two times larger (and plus one) than the tree with height - 1.

For tree with height = 2 we have 7 elements, for tree with height = 3 we have 7*2+1 = 15 elements.

Using this observation we build simple condition

i < array.length / 2

You can check this condition is valid for any non-leaf node in the tree.

img

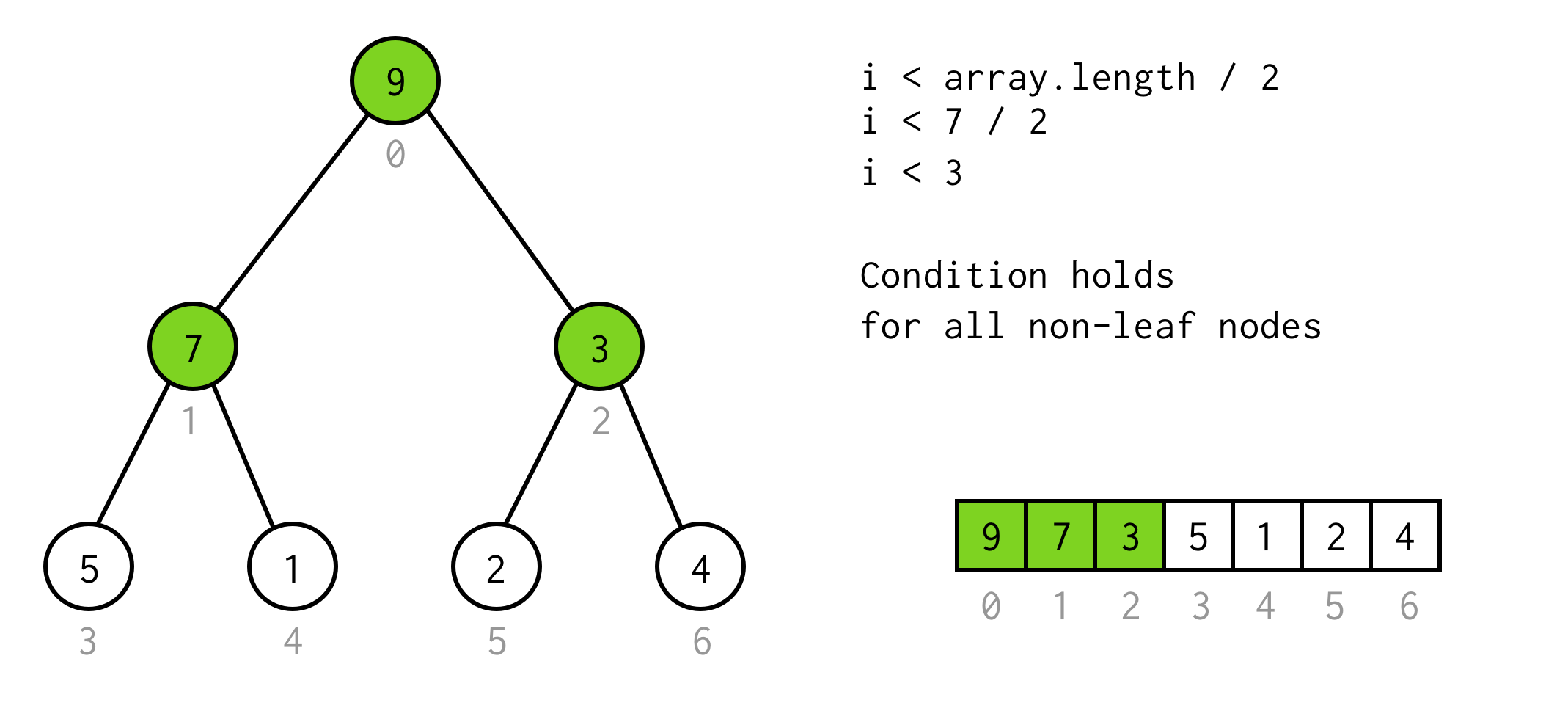
Nice so far. We can run doubling, and we even know when to stop. But this way we can check only left children of the nodes.

When we stuck at the leaf node and can not apply doubling anymore, we perform jump operation. Basically, if doubling is go to left child, jump is go to parent and go to right child.

img

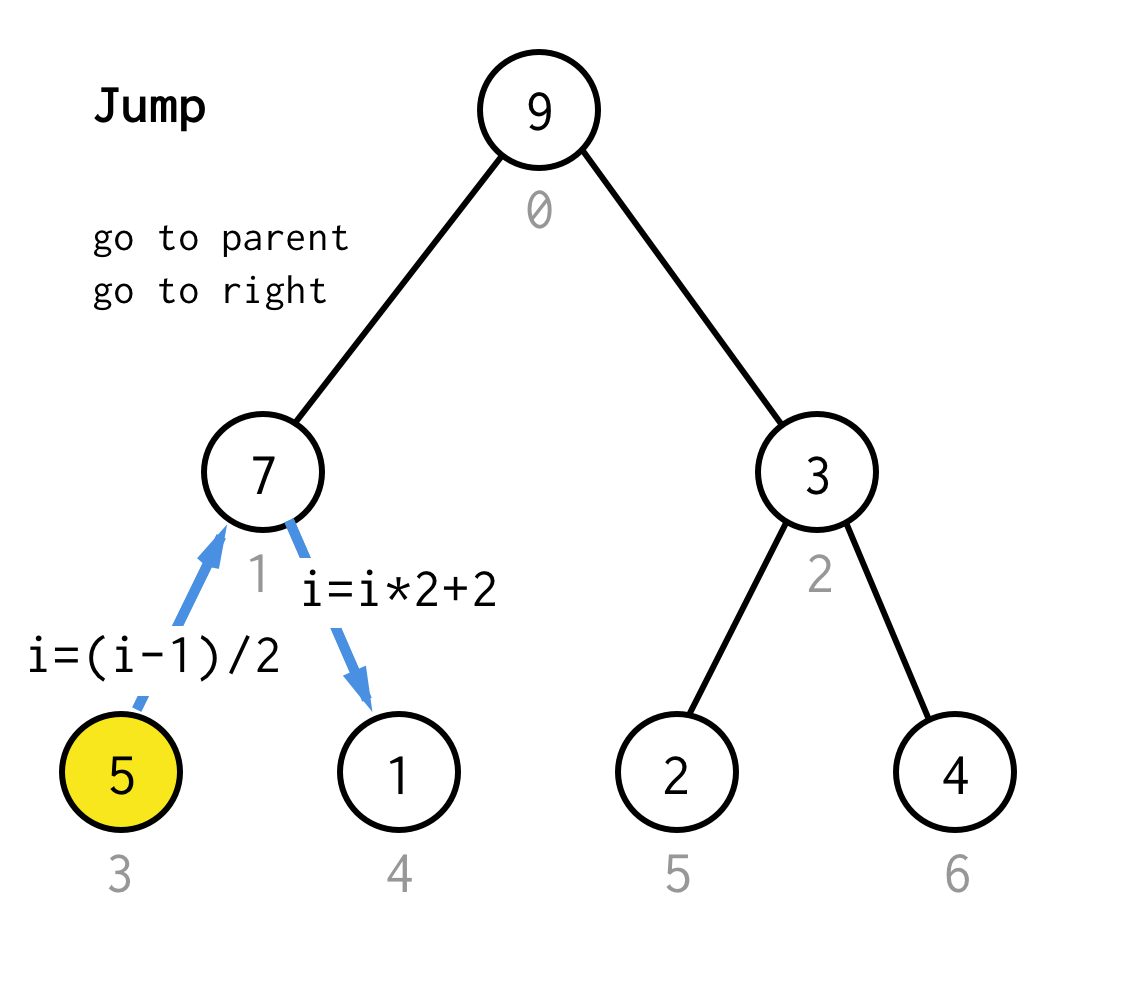
Such jump operation can be implemented by just incrementing the leaf index. But when we stuck at the next leaf node, increment doesn’t move node to the next node, required for DFS. So we need to do double jump

img

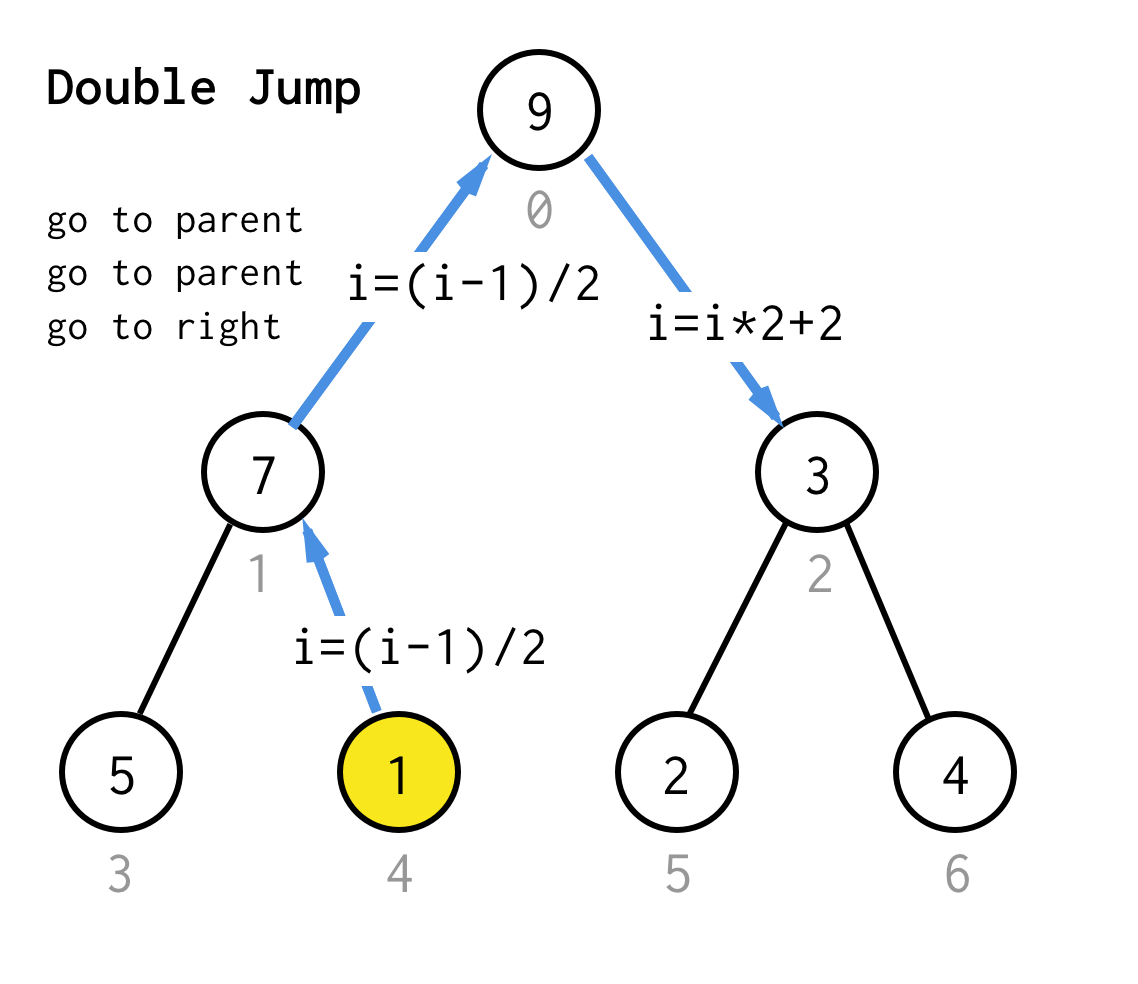
Make it more generic, for our algorithm we could define operation jump N, which specifies how many jumps to the parent it requires and always finishes with one jump to the right child.

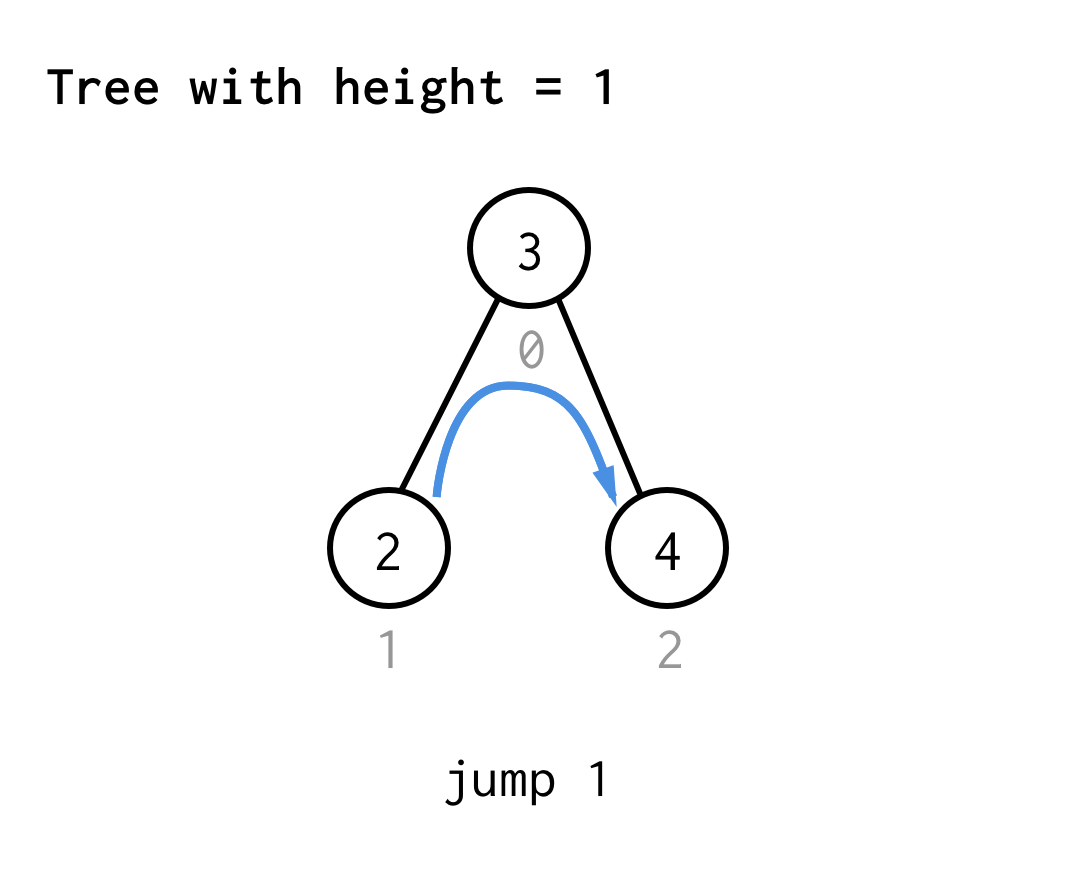
For the tree with height 1, we need one jump, jump 1

img

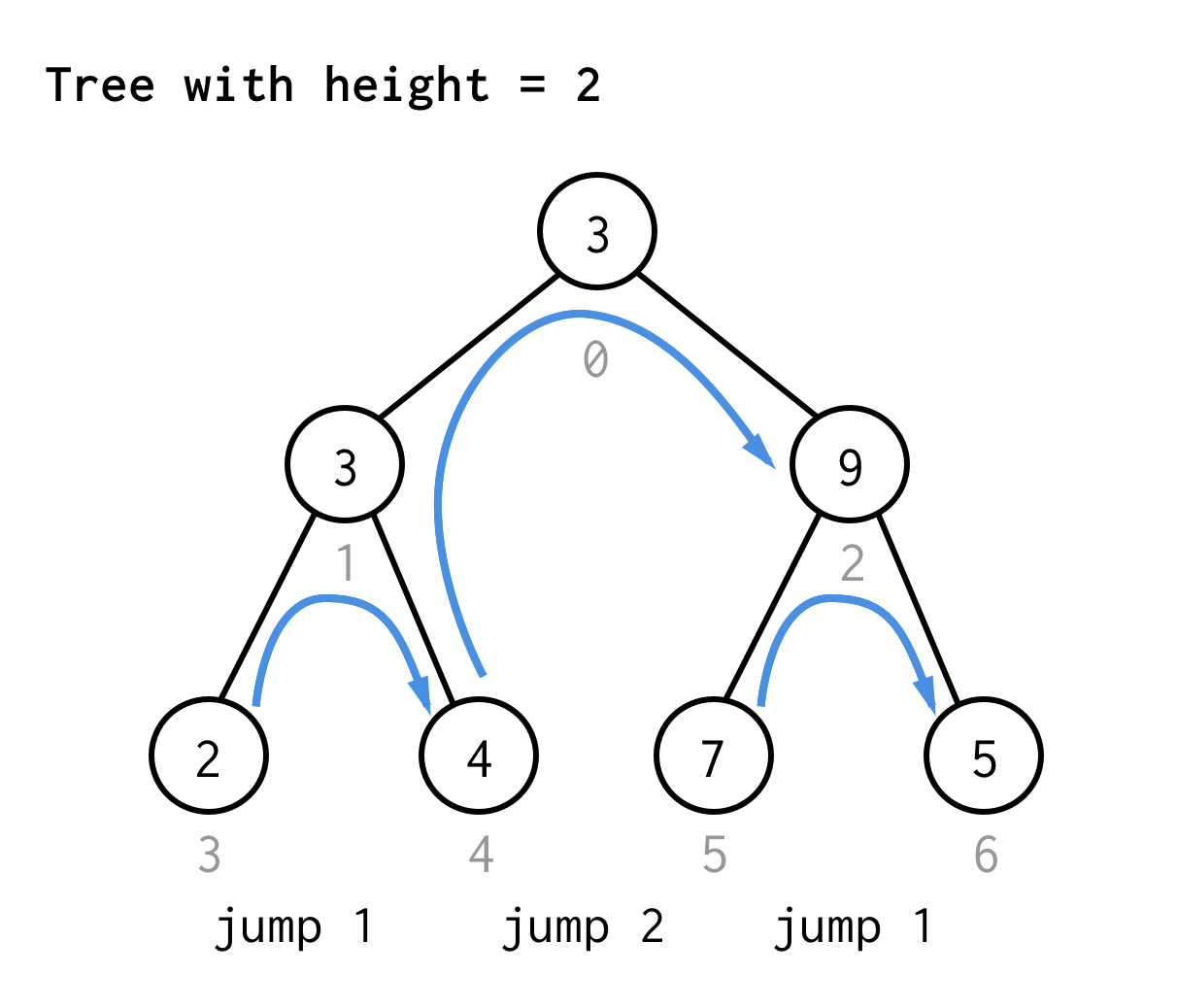
For the tree with height 2, we need one jump, one double jump, and than one jump again

img

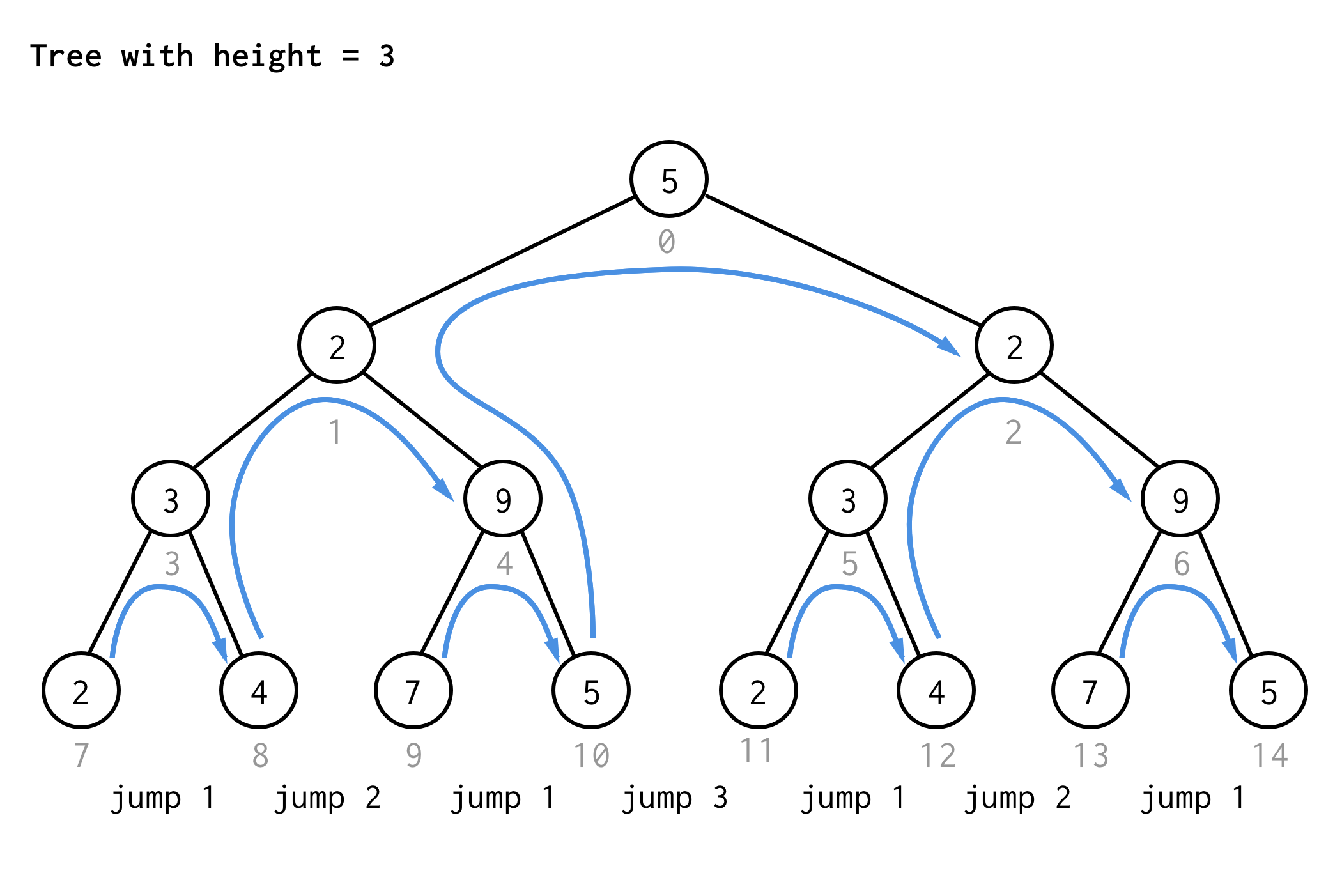
For the tree with height 3, you can apply the same rules and get 7 jumps.

img

See the pattern?

\[Jumps_{height} = Jumps_{height-1} \space{Height}\space Jumps_{height-1}\]

If you apply the same rule to the tree of height 4 and write down only jump values you will get next sequence number

1 2 1 3 1 2 1 4 1 2 1 3 1 2 1

This sequence known as Zimin words and it has recursive definiton, which is not great, because we not allowed to use recursion.

Let’s find some another way to calculate it.

If you look carefully at the jump sequence, you can see non recursive pattern.

img

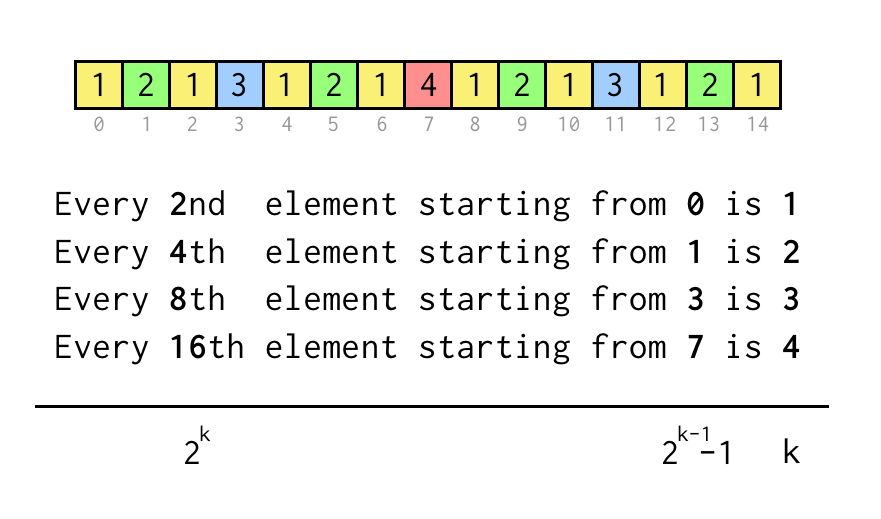
We can track index for current leaf j, which corresponds to the index in sequence array above.

To verify statement like “Every 8th element starting from 3” we just check j % 8 == 3, if it’s true three jumps to the parent node required.

Iterative jumping process will be following

If you putting all together what we’ve discussed

public int dfs(Predicate<T> predicate) {
    int i = 0;
    int leaf = 0;
    while (i < array.length) {
        if (array[i] != null && predicate.test(array[i])) return i; // node found
        if (i < array.length / 2) { // not leaf node, can be advanced
            i = 2 * i + 1; // try left child
        } else { // leaf node, jump
            int k = 1;
            while (true) {
                i = (i - 1) / 2; // jump to the parent
                int p = k * 2;
                if (leaf % p == k - 1) break; // correct number of jumps found
                k = p;
            }
            // after we jumped to the parent, go to the right child
            i = 2 * i + 2;
            leaf++; // next leaf, please
        }
    }
    return -1;
}

Done. DFS for binary tree array without stack and recursion

Complexity

The complexity looks like quadratic because we have loop in a loop, but let’s see what reality is.

Performance

Although theory is good, let’s see how this algorithm works in practice, comparing to others.

We test 5 algorithms, using JMH.

We’ve precreated a tree and using predicate to match the last node, to make sure we always hit the same number of nodes for all algorithms.

So, results

Benchmark                                Mode  Cnt         Score        Error  Units
------------------------------------------------------------------------------------
BinaryTreeBenchmarks.bfsOnArray         thrpt  200  91378159.672 ± 625885.079  ops/s
BinaryTreeBenchmarks.bfsOnBinaryTree    thrpt  200   7892439.856 ±  84124.694  ops/s
BinaryTreeBenchmarks.dfsOnArray         thrpt  200  19980835.346 ± 209143.115  ops/s
BinaryTreeBenchmarks.dfsOnBinaryTree    thrpt  200  13615106.113 ±  91863.833  ops/s
BinaryTreeBenchmarks.dfsOnStackOnArray  thrpt  200  11643533.145 ±  87018.132  ops/s

Obviously, BFS on array wins. It’s just a linear search, so if you can represent binary tree as array, do it.

Iterative DFS, which we just described in the article, took 2nd place and 4.5 times slower then linear search (BFS on array)

The rest three algorithms even slower then iterative DFS, probably, because they involve additional data structures, extra space and memory allocation.

And the worst case is BFS on Binary Tree. I suspect here the linked list is a problem.

Conclusion

Binary Tree Array is a nice trick to represent hierarchical data structure as a static array (contiguous region in the memory). It defines a simple index relationship for moving from parent to child, as well as moving from child to parent, which is not possible with classic binary array representation. Some drawbacks, like slow insertion/deletion exists, but I’m sure there are plenty applications for binary tree array.

As we have shown, search algorithms, BFS and DFS implemented on arrays are much faster then their brothers on a reference based structure. For real world problems it’s not so important, and, probably, I still will use the reference based binary array.

Anyway, it was a nice excercise. Expect question “DFS on binary array without recursion and stack” on your next interview.

mishadoff 10 September 2017
blog comments powered by Disqus