Clojure Euler: Problem 001
If we list all the natural numbers below 10 that are multiples of 3 or 5, we get 3, 5, 6 and 9. The sum of these multiples is 23.
Find the sum of all the multiples of 3 or 5 below 1000.
Permalink: http://projecteuler.net/problem=1
The simplest problem and nothing hard to solve it in standard iterative way (C-style pseudocode):
int s = 0;
for (int i=0; i < 1000; i++) {
if ((i % 3 == 0) || (i % 5 == 0)) s+=i;
}
We get result immediately. But loop that changes value of some variable it’s not a functional approach. Let’s rewrite this solution in recursive way in clojure:
(loop [i 0 s 0]
(if (= i 1000) s
(if (or (= 0 (mod i 3))
(= 0 (mod i 5))) (recur (inc i) (+ s i))
(recur (inc i) s))))
Just few words what we are doing here:
- loop - create binding between names and values in scope of loop body.
For now, think about loop like a function definition with two variables
iandsalong with calling such function with argumentsi=0, s=0.iis a loop counter,sis an accumulator variable that holds current sum. - mod - calculates remainder of division two numbers.
inc - increment value, similar to
(+ i 1). - Recursion base case: if we have
ivalue equals to1000, then we finished our work and return current accumulator values. Otherwise, - Recursion step: if current
ivalue is multiply of3or multiply of5, we add counter value to accumulator, increment loop counter and call this function with these new arguments. Otherwise, we just increment value and call function. This way we recursively go back to the first line of function with changed values until we get recursion base condition as true and return accumulator. Recursion call performed by recur.
This can be a bit harder to understand than iterative style, but we have a couple of pros there.
- There are no variables. There are values and names bound to that values. That means that we can’t change one value to another inside loop. That’s why we recursively call this function with changed values. Such trick helps to avoid hard-to-spot error-prone situations where iteration counter changed inside the loop.
- This is more flexible way than iteration. We can pass as much arguments as we want, move forward-backward, select dynamic iterative step and even select any stop condition.
- Safety. We are completely safe that our loop is pure local. It can not change anything outside. All garbage he left was cleared after returning value (Ecologists are very happy!)
Congratulations! Problem solved, but let’s find more elegant way.
We can split our problem into two simpler problems:
- Find sum of all multiples of
3below1000 - Find sum of all multiples of
5below1000 - Add these two sums
Stop, stop! What about numbers that multiples of 3 and multiples of 5, like 15, 30, 45,...? We add them twice.
Good catch. Let’s just subtract them once from total sum:
- Find sum of all multiples of
3below1000 - Find sum of all multiples of
5below1000 - Find sum of all multiples of
15below1000 - Add sum 1 to sum 2 and subtract sum 3.
You see the repeated “Find sum of all…“. It’s clear definition of function. Let’s implement it.
(defn sum-of [d] (reduce + (range 0 1000 d)))
One line! Excited? Brief description, what we wrote:
- defn indicates function definition.
We called function
sum-of, it accepts one argumentd(multiple of what?). As you, probably notice, we do not enforced to specify type of function argument, as well as function returning type. All it’s because clojure is dynamic language. Dynamic languages have pros and cons over static, but we omit their differences. For now. - reduce takes two parameters: function of two arguments and collection,
and applies that function to first two values, than to result and next value, again, again, until the end of collection.
So, for example
(reduce * [2 3 4 5])calculates(* 2 3)that is6, calls(reduce * [6 4 5]), then calls(reduce * [24 5])and finally returns120. - range function generates list. As you see it takes three parameters,
but there are overloaded versions that takes 2, 1 or even 0 values.
(range 0 1000 d)start generation from0, next value will beprevious plus d, until we exceed1000. Exclusively. So,(range 0 10 3)returns(0 3 6 9).
Ok. We have function “Find sum of all…” and almost all work is done. Just call this function with proper arguments and you’ll get the result:
(+ (sum-of 3) (sum-of 5) (- (sum-of 15)))
Done. In functional, clear, concise way in two lines of code.
Note: our algorithm complexity is O(n).
If we remember school course of math, we realize that all our sequences are arithmetic progressions.
That means for caluclating sum of sequence we don’t need count sum in usual way, we just can use formula:
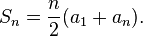
n is a count of numbers in a sequence, a1 - first value, an - last value.
Now we can reimplement our sum-of function next way:
(defn sum-of [d]
(let [a1 d
an (- 999 (mod 999 d))
n (quot 999 d)]
(/ (* cnt (+ a1 an)) 2)))
More harder to understand, but doable. New language syntax appears (999 used as we have “below 1000” in problem description):
- let - creates a lexical context for expression. In fact, it’s just separate block of code, with names, that exist only in scope of that block. After let we evaluates some expression and gives some values to the result.
a1- first element of sequence, just step valued.an- last element of sequence. We don’t know last element, so we need to calculate it. Little trick: find the remainder of division 999 by d, and subtract it from 999.n- count of numbers in a sequence. We also don’t know this value. It just will be integer number of division 999 by d. Exactly what quot function does.- And finally, the expression - formula for sum of arithmetic progression.
Actually, we reduced readability of our code, but improved algorithmic complexity from O(n) to O(1).
GitHub for lazy.
P.S. Programming not tied to some problem is nothing. That’s why, in first problem I prefer O(n) solution.
It still solves problem in appropriate time and have more readable code. If n grow, I’ll think about switching to O(1) strategy, but not for now.
Have fun!
mishadoff 12 October 2012